Sigmoid Function
$$f(x)=\left(\frac{1}{\left(1+\exp ^{-x}\right)}\right)-(1.4)$$
Sigmoid Function 在预测二分类问题上很成功,而且主要用于浅层的网络。当用随即小的值初始化神经网络时候,不应该用Sigmoid Function用于激活方程(AF)。
Sigmoid Function有一个主要的问题是,在深层网络反向传递时候梯度会非常的陡峭,有可能导致梯度饱和,slow convergence
Hard Sigmoid Function
$$f(x)=\max \left(0, \min \left(1, \frac{(x+1)}{2}\right)\right)-(1.6)$$
比sigmoid的主要好处是计算的时间会变小
Sigmoid-Weighted Linear Units (SiLU)
where $s=$ input vector, $z_{k}=$ input to hidden units $\mathrm{k}$. The input to the hidden layers is given by
$$
z_{k}=\sum w_{i k} s_{i}+b_{k}-(1.8)
$$
Silu只能用在隐藏层,只能用在强化学习基础的系统上,有时候会比RELU表现的还好
Derivative of Sigmoid-Weighted Linear Units (dSiLU)
$$a_{k}(s)=\alpha\left(z_{k}\right)\left(1+z_{k}\left(1-\alpha\left(z_{k}\right)\right)\right)-(1.9)$$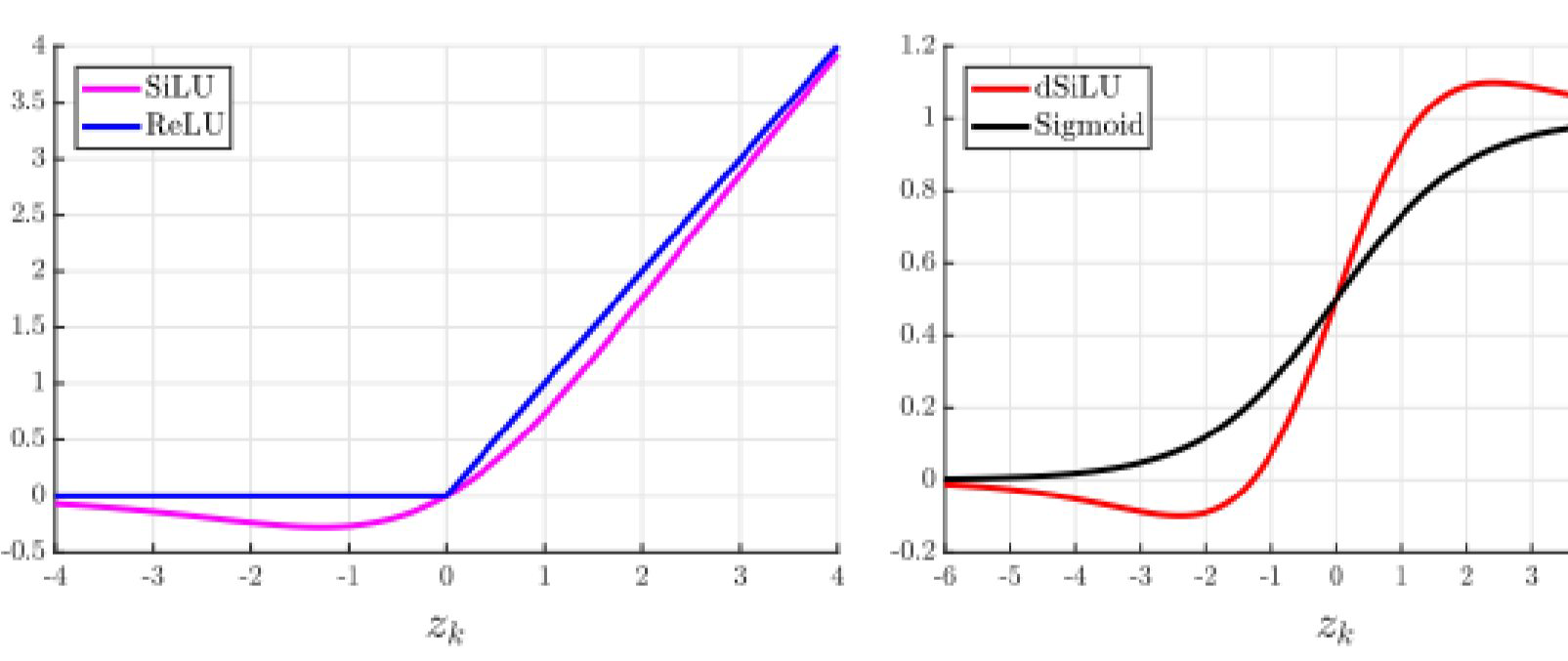
Tanh(Hyperbolic Tangent Function)
$$f(x)=\left(\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\right)-(1.10)$$
与sigmoid相比,在多层网络里面表现比较好,tanh能解决sigmoid的梯度消失的问题,主要原因是tanh输出的output是0-centered,所以反向传递的时候会好。
tanh在计算中会有一些死亡神经元出现,(可以由relu解决)
tanh主要用于recurrent神经网络在语言处理和语音识别的任务上。